Reed Solomon Decoder, Syndromes

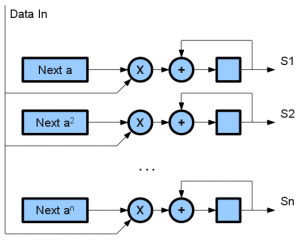
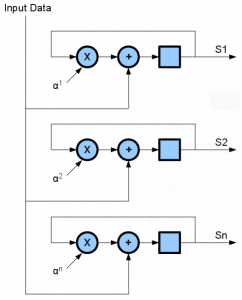
As mentioned, the first part of my Reed-Solomon decoder implementation is the calculation of syndromes.  This is a straightforward process that only requires a large amount of parallel processing. 

Syndrome Computation

The received message can be expressed as a polynomial.  For example, if 1, 2, 3, 4 is received, it could be interpreted as either or as .  For my decoder implementation, which I designed to work with my encoder, I chose the former.

As a polynomial, the value could be evaluated for different values of x.  The syndrome calculation is simply .

Alternate Syndrome Structure

The above is a direct implementation of the syndromes.  There is another, more hardware-efficient method.  It is based on performing the multiply on the previous accumulated value, instead of the input.  This would give:

Which would give .  The advantage to this is that the multiplication is a multiplication by a constant.  This uses less logic to implement, and is faster.

The importance of the syndromes is not immediately apparent.  The next steps will determine an LFSR (with coefficients in GF256) that can generate the sequence of syndromes.  This becomes the error locater polynomial.  Thus the pattern of syndromes shows where the errors are.  Within such an LFSR, there are several different possible initial states or “phases”.  The initial state of the LFSR will provide the error magnitudes.

The relevant code for this article is VHDL: Reed-Solomon Decoder Syndrome Calculation