Reed Solomon Decoder, Chein Search

The Berlekamp-Massey algorithm provides an error locater polynomial.  Similar to the syndromes, this polynomial doesn’t provide the required information directly.  Instead, it is the multiplicative inverse of the roots of this polynomial that correspond to the error locations.  Just like integers, general factoring of polynomials is not a simple task.  The task is simplified by making assumptions about the polynomial though.

For codewords 255 elements or less, the roots of the error locater polynomial fall to simple factors of .  The chein search simply evaluates the error locater polynomial, , at all valid values of .  This can be done using similar hardware as the previous stages.

Chein Search Hardware

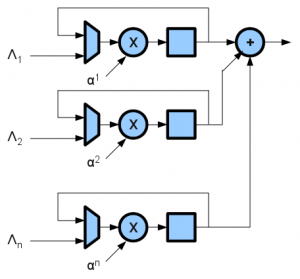
A set of repeated multiply elements can be used with the N-input XOR gate summation circuit to evaluate efficiently.  The coefficients of the non-zero degree elements of the error locater are loaded into this array first.  From here, Galois-Field multiply by constant circuits are used to perform the multiplies.  The summation circuit XORs all of the non-zero terms with the zero’th degree term, which is always .

In my implementation, I load the array with the error locater, multiplied by the powers of first.  This allows the first element to be evaluated to be , and the last to be .  This allows the inverses of the roots to be detected in-order, which will have desirable properties later.  The roots are detected when the large summation is equal to zero.

The code for this article is:

• VHDL: Reed-Solomon Decoder Chein Search
• VHDL: Reed-Solomon Decoder Chein Search Logic
• Python: Code generator for Chein search